Cuerpos geométricos.
Un cuerpo geométrico es un elemento que existe en la realidad o que somos capaces de concebir, el cual ocupa un volumen en el espacio, es decir, tiene tres dimensiones (ancho, alto y largo) a diferencia de las figuras, las cuales no tienen volumen.
Un cuerpo geométrico es un elemento que existe en la realidad o que somos capaces de concebir, el cual ocupa un volumen en el espacio, es decir, tiene tres dimensiones (ancho, alto y largo) a diferencia de las figuras, las cuales no tienen volumen.
Llamamos cuerpos geométricos a los sólidos que ocupan un lugar en el espacio. Es decir que los podemos tocar, medir y pesar.
Las medidas se toman en longitud, anchura y altura.
Los cuerpos geométricos se dividen en dos grupos: poliedros y los cuerpos redondos.
VOLÚMENES DE LOS CUERPOS GEOMÉTRICOS
Cuando estudiamos las áreas hablábamos de dos dimensiones: largo y ancho. El producto de los valores largo X ancho nos da el área.
Para calcular un volumen necesitamos tres dimensiones: largo, ancho y alto.El producto de los valores largo X ancho X alto nos da el volumen.
Es lo mismo que decir, el volumen lo calculamos también multiplicando el área de la base por la altura.
Objetivo:
- El objetivos es de conocer y aplicar las formulas para obtener el volumen de los cuerpos geométricos.
- Resolver problemas relacionados con encontrar el volumen de un cuerpo geométrico.
Ejercicio: calcular el volumen de un cubo cuya arista mide 9 cm
En este ejercicio vamos a aplicar la formula de dicha figura, asi:
V=9*9*9= 729
El resultado es V= 729cm³
Volumen Prisma Rectangular
Esta figura tiene ancho, largo y altura
Ejercicio: Hallar el volumen de un prisma rectangular que tiene de largo 40 cm, de ancho 25 cm y de altura 30 cm
En la formula nos indica que debemos multiplicar 40*25*30 y eso es igual a 30,000
En la formula nos indica que debemos multiplicar 40*25*30 y eso es igual a 30,000
V= 40*25*30= 30,000
V= 30,000 cm³
Volumen Octaedro
 →a= 6 cm
→a= 6 cm
La formula es raíz cuadrada de 2 * la ″a′′ al cubo sobre 3
Y esto se miraría así:
V= √26³÷3= 1.4142*216÷3
↑
arista
=101.8224
V= 101.8224cm³
Volumen Tetraedro
Para sacar el volumen de tetraedro tenemos que sacar raíz cuadrada de 2 multiplicarla por la arista al cubo y dividir el resultado entre 12
Ejercicio: calcular el volumen de un tetraedro cuya arista mide 12 cm
 a= 12 cm
a= 12 cm
Vamos a sacar la raíz cuadrada de 2 por 12 al cubo dividiéndola entre 12, la raíz de 2 es 1.4142 por 12 al cubo que es 1728 entre 12 y el resultado seria así:
V= √2*12³÷12 = 1.4142*1728÷12= 203.6448
V= 203.6448cm³
Volumen Pirámide
 h= altura
h= altura
l= lado
AB= (24*3) / 2 = 36 cm
 h= altura
h= altura
 h= 12 cm
h= 12 cm
Volumen Octaedro
Formula: V√2a³÷2
Ejercicio: Calcular el volumen de un octaedro cuya arista mide 6 cm
 →a= 6 cm
→a= 6 cmLa formula es raíz cuadrada de 2 * la ″a′′ al cubo sobre 3
Y esto se miraría así:
V= √26³÷3= 1.4142*216÷3
↑
arista
=101.8224
V= 101.8224cm³
Volumen Tetraedro
Para sacar el volumen de tetraedro tenemos que sacar raíz cuadrada de 2 multiplicarla por la arista al cubo y dividir el resultado entre 12
se encuentran)
Formula: V= √2a³÷12Ejercicio: calcular el volumen de un tetraedro cuya arista mide 12 cm
 a= 12 cm
a= 12 cmVamos a sacar la raíz cuadrada de 2 por 12 al cubo dividiéndola entre 12, la raíz de 2 es 1.4142 por 12 al cubo que es 1728 entre 12 y el resultado seria así:
V= √2*12³÷12 = 1.4142*1728÷12= 203.6448
V= 203.6448cm³
Volumen Pirámide
 h= altura
h= altural= lado
Para sacar el volumen de una pirámide debemos encontrar el área de la base que es lado por lado ya que la base es un cuadrado multiplicarla por la altura y dividirlo entre 3
Formula: V= Ab*h ÷3
Ejercicio: calcular el volumen de una pirámide que mide 12 cm de altura y de lado 8 cm
l= 8 cm
 h=altura
h=altura
 h= 21cm
h= 21cm
 r= radio
r= radio
 r= 24 cm
r= 24 cm
 l= lado
Ejercicio: Calcular el volumen del prisma hexagonal del prisma hexagonal cuyo apotema mide 3 cm, su altura 10 cm y cada lado mide 4 cm
l= lado
Ejercicio: Calcular el volumen del prisma hexagonal del prisma hexagonal cuyo apotema mide 3 cm, su altura 10 cm y cada lado mide 4 cm
 l= 4 cm
l= 4 cm
PB= 6*4 = 24cm
Vamos a multiplicar 8*8 que es = 64, luego multiplicarlo por la altura que es 12, seria 64*12 = 768 y dividirlo entre 3 768÷3 = 256
AB= 8*8 = 64
V= 64*12 ÷3 = 768÷3 =256
V= 256 cm³
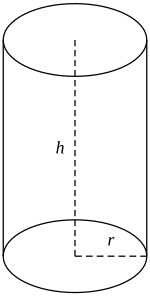
Volumen de Cilindro
Para sacar el volumen de un cilindro tenemos que obtener el área de la base y como en este caso la base es un circulo su área es 𝛑*r² y el resultado del area del circulo lo multiplicamos por su altura
 h=altura
h=altura
r= radio
Formula: 𝛑r²*h
𝛑= 3.1416
Entonces si calculamos el volumen de un cilindro que tiene el radio 12 cm y de altura 21 cm, multiplicamos 3.1416 * 12² es = a 144* 21 es = 9500.1984
Ejercicio:
V= 3.1416*12²*21 = 144
=3.1416*144*21=9500.1984
El resultado es:
V=9500.1984cm³
 h= 21cm
h= 21cm
r= 12cm
Volumen Esfera
Para sacar el volumen de una esfera hay que utilizar la formula:
V= 4÷3*𝛑*r³
Ejercicio:
Calcular el volumen de una esfera cuyo radio es de 24 cm
Y esto vamos dividir 4 sobre 3que es = 1.333 * 3.1416 (que es el valor de) 𝛑 * 24³ es = 13824
luego realizamos las multiplicaciones y obtenemos como resultado:
V=57905.97 cm³
Volumen Prisma
Para sacar el volumen de cualquier porque hay varios tipos de Prisma hay que calcular primero el área de la base que es:
- Perimetro de la Base* el Apotema entre 2
- En segundo lugar calculamos el volumen multiplicando el área de la base* la altura del Prisma.
 l= lado
l= lado
h= altura
a= apotema
 l= 4 cm
l= 4 cm
h= 10 cm
a= 3 cm
Lo primero que vamos a hacer es calcular el área de la base para ello hay que obtener el perímetro de la base multiplicando el numero de lados * la medida de cada lado:
Después obtenemos el área de la base multiplicando 24 * 3 y diviendolo entre 2:
Por ultimo multiplicamos el área de la base * la altura:
36 *10=360
V= 360cm³
Volumen Cono
r= radio
Formula:
V= 1÷3 * 𝛑 * r² * h
Ejercicio: Calcular el volumen de un cono cuyas medidas son r= 10 cm y altura= 12 cm
r= 10
Multiplicamos 3.1416 * 10² * 12
V= 1/3 * 3.1416 * 10² * 12
El cuadrado de 10 = 100 * 3.1416 * 12
V= 1/3 * 3.1416 * 100 * 12
Lo que nos sale es 1256.64 cm³
V= 1/3 * 3.1416 * 10² * 12
V= 3769.92 / 3 = 1256 cm³
Hasta que Finalizamos, muchas gracias ✌

